1212. Infinite Sequence - 2

Define an infinite sequence A as follows:

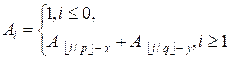
Given the values n, p, q, x and y, compute A_n.

Input. Five integers n, p, q, x, y (0 £ n £ 10¹³, 2 £ p, q £ 10⁹, 0 £ x, y £ 10⁹).

Output. Print the value of A_n.

Sample input 1	Sample output 1
12 2 3 1 0	8
Sample input 2	Sample output 2
10000000 2 3 10000000 10000000	2

SOLUTION

recursion

Algorithm analysis

Since n £ 10¹³, storing all values A_i (i = 0, 1, …, n) is impossible, either using an array or a map structure due to memory limitations. Therefore, we’ll use recursion defined by the recurrence relation for computations.

At the same time, the values A_i for i < 5000000 will be stored in the array m to avoid repeated computations and speed up the program.

Algorithm implementation

To store the values A_i (i < 5000000), declare an array m.

#define MAX 5000000

long long m[MAX];

The function f computes the value of A_n.

long long calc(long long n, long long p, long long q,

long long x, long long y)

{

If n £ 0, then A_n = 1.

if (n <= 0) return 1;

If n < 5000000 and the value m[n] is already computed (is not zero), return it.

if ((n < MAX) && m[n] > 0) return m[n];

Perform a recursive computation of A_n according to the formula provided in the problem statement.

long long temp = calc(n/p-x,p,q,x,y) + calc(n/q-y,p,q,x,y);

If n < 5000000, store the result A_n in the array m to avoid repeated computations in the future.

if (n < MAX) m[n] = temp;

return temp;

}

The main part of the program. Read the input data.

scanf("%lld %lld %lld %lld %lld",&n,&p,&q,&x,&y);

Compute and print the answer.

res = calc(n,p,q,x,y);

printf("%lld\n",res);

Java implementation

import java.util.*;

public class Main

{

static int MAX = 5000000;

static long m[] = new long[MAX];

public static long f(long n, long p, long q, long x, long y)

{

if (n <= 0) return 1;

if (n < MAX && m[(int)n] > 0) return m[(int)n];

long temp = f(n/p-x,p,q,x,y) + f(n/q-y,p,q,x,y);

if (n < MAX) m[(int)n] = temp;

return temp;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long n = con.nextLong();

long p = con.nextLong();

long q = con.nextLong();

long x = con.nextLong();

long y = con.nextLong();

long res = f(n,p,q,x,y);

System.out.println(res);

con.close();

}

}

Python implementation

To store the values A_i (i < 5000000), declare a list m.

MAX = 5000000

m = [0] * MAX

The function f computes the value of A_n.

def f(n, p, q, x, y):

If n £ 0, then A_n = 1.

if n <= 0:

return 1

If n < 5000000 and the value m[n] is already computed (is not zero), return it.

if n < MAX and m[n]:

return m[n]

Perform a recursive computation of A_n according to the formula provided in the problem statement.

temp = f(n // p - x, p, q, x, y) + f(n // q - y, p, q, x, y)

If n < 5000000, store the result A_n in the array m to avoid repeated computations in the future.

if n < MAX: m[n] = temp

return temp

The main part of the program. Read the input data.

n, p, q, x, y = map(int, input().split())

Compute and print the answer.

res = f(n, p, q, x, y)

print(res)